計算複雑性理論をなんとなく理解してパフォーマンスを改善する

どうも, みゅーとんです.

今回はパフォーマンスチューニングの総集編に当たる記事になります.

以前 OSS として公開しているライブラリ json-origami のバージョンアップで大幅にパフォーマンスを悪くしてしまい, 製品に影響が出てしまったので, その改善のための観点として, 計算量をちゃんと見積もってみようと思いました.

関連記事

以下の記事は, この本記事で取り上げる json-origami の改善まわりで実施した, 品質担保まわりの取り組みです. こちらも合わせて, 軽く読んでおくことをおすすめします. techblog.hacomono.jp techblog.hacomono.jp techblog.hacomono.jp

概要

3 行でまとめ

• 計算複雑性理論 (計算量のオーダーなどと称される) の概念は, 実際パフォーマンス改善のためにコードを良くする際に参考にはなる.
• 理論をある程度理解していても, 実際のコードから厳密に計算は困難.
• 計算量を上げる要因となる変数が何であるかを見立てて, 最悪のケースを算出する.

取り上げないこと

計算複雑性理論については軽く触れますが, 深く掘り下げると収集がつかないので, 概要にとどめます.

まだ計算量概念については学習中であるため, 間違いは多く有りえます.

逃げの一言になってしまいますが, 本記事で紹介するのは, あくまで “改善のために着目した観点” です. また, まさかりを受け付けてます. ぜひバッサリと切り落としてほしいです.

背景

インシデント未遂を引き起こしてしまいました.

hacomono-lib で公開している OSS の json-origami にて, パッチバージョンアップとして, たった１行変更するだけのバグ修正を行いました.

この修正が計算量を膨大に引き上げてしまい, プロダクトのコードでパフォーマンスが大幅劣化してしまいました.

暫定対処として, 利用する json-origami のバージョンを下げるなどの対応はしましたが, 恒久対処として, json-origami のロジックを見直してみると, どうやら書き直しが必要な規模感を感じたため, 思い切ってしっかり対応してみることにしました.

json-origami とは ?

今回は具体的なロジックの話になるため, 修正対象の json-origami ライブラリについて説明します. リポジトリはこちら. github.com

npm 向けのパッケージとして公開しているライブラリで, 深い階層のオブジェクトを, 割りと簡単に構造変更する汎用ロジックを提供しています.

例えば, { 'a.b.c': 'x.y.z' } のようなキーを元のオブジェクトのキー文字列, 値を変換後のオブジェクトのキーの文字列としたマップオブジェクトと, 変換対象のオブジェクトを渡すと写像変換をする twist 関数なんかがあったりします. 背景説明にて, パフォーマンスが劣化したのもこれです.

なんとなく, おっきい形の変更をする構図が折り紙みたいだなーと思い, json-origami と命名しました. API 詳細は README.md を確認してください.

計算複雑性理論 とは ?

wikipedia の引用になってしまいますが, 計算複雑性理論とは, 概要として

「あるアルゴリズムへの入力データの長さを増やしたとき、実行時間や必要な記憶量はどのように増えるか？」という問に答える理論

と説明されます.

この理論では, チューリング機会やら P, NP などの概念がありますが, 我々実際にプログラムを書く者からすると, この理論の中で特に “計算量のオーダー” が最もよく聞くと思います.
今回はその計算量のオーダーについて触れていきます.

計算量 とは ?

入力データ長を $N$ とするとき, その結果発生する処理時間や必要な記憶量については , 一般的に $O(N)$ のように表されます.

例えば,

• $O(1)$ .. 入力のサイズに応じず, 固定である
• $O(N)$ .. 入力サイズの大きさに比例して, 時間もしくは記憶量が増加する
• $O(N^{2})$ .. 入力サイズの大きさについて 2 乗する形で, 時間もしくは記憶量が増加する

というような意味合いです.
入力に応じて増減する時間を 時間計算量, 増減する記憶量を 空間計算量 と称されます.

ロジックに書くとわかりやすいかもしれないですね. 時間計算量の目安として, 以下は $O(N)$

for (let i = 0; i < input.length; i++) {
  // do something
}

以下は $O(N^{2})$ です.

for (let i = 0; i < input.length; i++) {
  for (let j = 0; j < input.length; j++) {
    // do something
  }
}

また, 計算量のオーダーでは, N に対する定数倍や指数の少ない項は省略されます.
例えば, 以下は $O(2N^{2} + N)$ っぽいですが, 省略して $O(N^{2})$ が正になります.

for (let i = 0; i < input.length; i++) {
  for (let j = 0; j < input.length; j++) {
    // do something
  }

  for (let j = 0; j < input.length; j++) {
    // do something
  }
}

for (let j = 0; j < input.length; j++) {
  // do something
}

空間計算量のサンプルを示すと, 以下は $O(N)$

const arr = Array(input.length)

以下は $O(N^{2})$ です.

const arr = Array(input1.length)
for (let i = 0; i < input1.length; i++) {
  arr[i] = Array(input2.length);
}

空間計算量でも同様に, 定数倍や指数の少ない項目を省略します. 以下は $O(N^{2})$ です.

const arr1 = []
const arr2 = []
for (let i = 0; i < input.length; i++) {
  for (let j = 0; j < input.length; j++) {
    arr1.push(getData1(i, j))
  }
  arr2.push(getData2(i))
}

少ない項や定数倍を省略する理由は単純で, $N$が無限の極限をとっていく程度に極端に大きい数にしたとき, 定数倍や小さい項は計算量に大きな変化を与えなくなるためです.

概要説明はこれくらいにしておきます. 理論の理解にあたって, 以下はだいぶ参考になった記事でした. (ありがとうございました)

qiita.com qiita.com

計算量 from Ken Ogura

www.slideshare.net

課題

json-origami の実際のコードを確認して, 計算量を求めてみます.

今回パフォーマンス劣化を起こしてしまった twist 関数のコードは以下の通り.

import { fold } from './fold'
import type { Dictionary, MoveMap, Twist, TwistOption } from './type'
import { unfold } from './unfold'
import { includesKey } from './utils'

export function twist<D extends Dictionary, M extends MoveMap<D>>(
  obj: D,
  moveMap: M,
  option?: TwistOption,
): Twist<D, M> {
  const folded = fold(obj, option)

  const twisted = Object.fromEntries(
    Object.entries(folded).map(([key, value]) => {
      const found = Object.keys(moveMap).find((k) => includesKey(key, k, option))

      if (found) {
        const newKey = key.replace(found, moveMap[found]!)
        return [newKey, value]
      }

      return [key, value]
    }),
  )

  return unfold(twisted, option)
}

twist 関数は, 第 1 引数のオブジェクトが例えば { a: { b: { c: 'd' }}} だったとして, 第 2 引数で { "a.b.c": "x.y.z" } を指定すると, 返り値は { x: { y: { z: 'd' }}} となる, 簡単に言うとオブジェクトの写像をするような処理になっています.

ざっくりまとめると, fold unfold 中間処理 の 3ブロックがあり, そのなかで最大の計算量を求める必要があります.

軽く調べた感じ、それぞれ以下の通りでした

fold の計算量

export function fold<D extends Dictionary>(obj: D, option?: FoldOption): Folded<D> {
  if (Object.keys(obj).length <= 0) {
    return {}
  }

  return Object.fromEntries(
    flatEntries(option?.keyPrefix ?? '', obj, {
      ...defaultCommonOption,
      ...option,
    } as FixedFoldOption),
  ) as Folded<D>
}

const arrayKeyMap = {
  dot: (prefix: string, index: number) => (prefix === '' ? `${index}` : `${prefix}.${index}`),
  bracket: (prefix: string, index: number) => `${prefix}[${index}]`,
} satisfies Record<ArrayIndex, (prefix: string, index: number) => string>

function flatEntries(key: string, value: object, opt: FixedFoldOption): [string, Primitive][] {
  if (value === undefined || value === null) {
    return []
  }

  const appendKey = (k: string | number) =>
    typeof k === 'number' ? arrayKeyMap[opt.arrayIndex](key, k) : key === '' ? k : `${key}.${k}`

  if (Array.isArray(value) && value.length > 0) {
    return value.flatMap((v, i) => flatEntries(appendKey(i), v, opt))
  }

  if (typeof value === 'object' && Object.keys(value).length > 0) {
    return Object.entries(value as object).flatMap(([k, v]) => flatEntries(appendKey(k), v, opt))
  }

  return [[key, value]]
}

fold 関数は { a: { b: { c: "d" }}} のようなオブジェクトを { "a.b.c": "d" } のような形に直します.

複数のループのネストはあるものの, 合計すると json object におけるプリミティブな値の数しか処理を実行していません. したがって, json object のプリミティブな値の数を $N$ とおくとして, fold 関数の時間計算量は $O(N)$ といえます.

json object の階層の数だけ再帰処理を行っており, その度に javascript の新しいスコープが発生することから, 階層の数を $D$ とおくとして, $O(D)$ といえるでしょう.

unfold の計算量

export function unfold<Kv extends Folded<any>>(kv: Kv, option?: UnfoldOption): Unfolded<Kv> {
  const fixedOpion = {
    ...defaultUnfoldOption,
    ...option,
  } as FixedUnfoldOption
  validateKeys(kv)

  return unfoldInternal(Object.entries(kv), fixedOpion) as Unfolded<Kv>
}

function unfoldInternal(entries: [string, unknown][], opt: FixedUnfoldOption): unknown {
  if (entries.length <= 0) {
    return {}
  }

  const firstKey = extractHeadKey(entries[0]![0], opt)

  if (firstKey === '') {
    return entries[entries.length - 1]![1]
  }

  if (typeof firstKey === 'number') {
    const maxIndex = entries
      .map(([key]) => extractHeadKey(key, opt) as number)
      .reduce((acc, index) => Math.max(acc, index), 0)

    const array = new Array(maxIndex + 1).fill(undefined).map((_, index) => {
      const filteredEntries = entries.filter(([key]) => extractHeadKey(key, opt) === index)

      if (filteredEntries.length <= 0) {
        return undefined
      }

      const unfolded = unfoldInternal(
        filteredEntries.map(([key, value]) => [omitHeadKey(key, opt), value]),
        opt,
      )

      return unfolded
    })

    if (opt.pruneArray) {
      return array.filter((v) => v !== undefined)
    }

    return array
  }

  const keys = Array.from(new Set(entries.map(([key]) => extractHeadKey(key, opt) as string)))
  return keys.reduce((acc, key) => {
    const filteredEntries = entries.filter(([k]) => extractHeadKey(k, opt) === key)
    const unfolded = unfoldInternal(
      filteredEntries.map(([k, value]) => [omitHeadKey(k, opt), value]),
      opt,
    )

    return {
      ...acc,
      [key]: unfolded,
    }
  }, {})
}

正直なんでこんなコード書いたんだろう・・っていう気がします.

unfold 関数は { "a.b.c": "d" } のようなオブジェクトを { a: { b: { c: "d" } } } のような形に直す処理をしています.

こちらも再帰処理がありますが, json object のプリミティブ値の数のループがあり, それをフィルタした数だけ再帰に突入しています.

再帰のたびにループ回数が減少します. 具体的な計算は困難であるため, 適当に最悪のケースで時間計算量を考え, $O(N^{D})$ とみなして良さそうです.

また, fold と同様に再帰のたびにスコープが生まれるため, 空間計算量は $O(D)$ と考えて良さそうです.

中間処理の計算量

再掲ですが, twist 関数は以下のコードでした.

import { fold } from './fold'
import type { Dictionary, MoveMap, Twist, TwistOption } from './type'
import { unfold } from './unfold'
import { includesKey } from './utils'

export function twist<D extends Dictionary, M extends MoveMap<D>>(
  obj: D,
  moveMap: M,
  option?: TwistOption,
): Twist<D, M> {
  const folded = fold(obj, option)

  // ここから中間処理
  const twisted = Object.fromEntries(
    Object.entries(folded).map(([key, value]) => {
      const found = Object.keys(moveMap).find((k) => includesKey(key, k, option))

      if (found) {
        const newKey = key.replace(found, moveMap[found]!)
        return [newKey, value]
      }

      return [key, value]
    }),
  )
  // ここまで中間処理

  return unfold(twisted, option)
}

export function includesKey(
  origin: string,
  match: string | RegExp,
  { arrayIndex }: CommonOption = defaultCommonOption,
): boolean {
  if (match instanceof RegExp) {
    return match.test(origin)
  }

  const split = (key: string): string[] => {
    const fixedKey = arrayIndex === 'bracket' ? key.replace(/\[(\w+)\]/g, '.$1') : key
    return fixedKey.split('.')
  }

  const originKeys = split(origin)
  const keys = split(match)

  if (keys.length > originKeys.length) {
    return false
  }

  const targets = originKeys.slice(0, keys.length)
  return targets.join('.') === keys.join('.')
}

ここの中間処理で, fold 結果のキーを写像先のキーに変換しています. この結果を unfold すればほしい結果が得られるという算段です.
だいぶぐるぐる回ってるのが見て取れますね.

includesKey は文字列をオブジェクトキーに見立てた場合の前方一致を見ています. includesKey の引数が RegExp のケースは twist 関数から呼ばれるケースでは利用されていないため無視します.

split は key の文字列長に対して線形の時間計算量であるため, includesKey は入力の origin の文字列長を $n$ , match の文字列長を $m$ とおいた際に $O(n + m)$ と考えられます.

ここで引数となる文字列は origin, match ともに "a.b.c" のような結合された文字列であるため, オブジェクトの深さ $D$ と, 変換元オブジェクトの平均的なキー文字列長 $L$ に置き換えて, $O(LD)$ としてしまったほうが, 結果がわかりやすそうです.

中間処理では, fold 結果の値数と 写像用の key-value オブジェクトのキー数の二重ループ構造で includesKey をコールしています. fold 結果はすなわち変換対象のオブジェクトの値数に同じであるため, 写像対象の値数を $M$ とおくことで, 時間計算量を $O(NMLD)$ としてよさそうです.

空間計算量については, 単純に変数を見れば良さそうなので, 時間計算量と同様の $O(LD)$ としました.

合算

まとめると, まず考慮すべき変数として以下があります

• $N$ .. 変換元となるオブジェクトにおけるプリミティブな値の総数
• $M$ .. 写像対象とするキーの数
• $D$ .. 変換元となるオブジェクトのネスト数
• $L$ .. 全キーの文字列長の平均

twist を構成する 3 つの処理における計算量は以下のとおりでした

• fold
  • 時間計算量 .. $O(N)$
  • 空間計算量 .. $O(D)$
• 中間処理
  • 時間計算量 .. $O(NMLD)$
  • 空間計算量 .. $O(LD)$
• unfold
  • 時間計算量 .. $O(N^{D})$
  • 空間計算量 .. $O(D)$

上記より, それぞれの和から係数の少ない項を排除すると, 時間計算量は

$$ O(N) + O(NMLD) + O(N^{D}) = O(NMLD + N^{D}) $$

空間計算量は

$$ O(D) + O(LD) + O(D) = O(LD) $$

となりました. 時間計算量がとにかくヤバいですね.

なぜプロダクトのコードでパフォーマンス劣化が起きたか?

単純な話で, D が 10 ~ 11 くらいあるキーがありました. 探せばもっと大きいかも.

また, 実は javascript における RegExp が, ただの String の関数を呼ぶ場合と比べると少し重めであることも最大の原因の一つでした. 中間処理では正規表現による処理を $O(NM)$ 回コールしていることになります.

どう改善すべきか？

基本的に, twist 関数については以下を考慮して処理を改善すべきと判断しました.

• unfold を使わない
• 正規表現を使わない

また, twist 関数に限らず, 全体的に以下を考慮して同様に修正すべきと考えました.

• ネストとループを組み合わせない
• キャッシュを考慮できるロジックを考えるべき
• 空間計算量はもう少し贅沢に使って良い. ただしちゃんと開放されたか確認する.

今回のインシデント未遂をうけて, このパフォーマンス改善のために, すべて書き直す対応を入れることにしました.

改善に際し, ロジックの書き直しに際し, ユニットテストは元々十分にありました. また, 改善が確認できるように, パフォーマンステストを事前導入し, 改善前後での差を確認しながら取り組みました.

改善のアイデア

そもそも twist 関数以外にも, 以下の問題が同様にありました.

• 基本的な処理は fold → 中間処理 → unfold で実現される
• 処理が全般的に愚直なため, キャッシュの戦略を立てれない

そのため, 以下の要件を満たすようなオブジェクトを作り, 各関数はこれを用いて結果のオブジェクトを作るように変更しました.

• ネストされたオブジェクトを内包する
• "a.b.c" のようなキーに対して get, set の処理ができる
• set においては, 途中のキーに対応するオブジェクトがない場合は都度新規に作成する
• 途中まで同じキーに対するアクセスをキャッシュによって省略する

そのときの修正の PR は以下です. 説明すると膨大になるため, 省略します. github.com

改善の結果

オブジェクトのプリミティブ値の数 $N$ に対して, 変更前後でのパフォーマンスを計測した結果, 以下のグラフのようになりました.

計測には tinybench を使用しています.

緑線が途中までしか記録されていないのは, 個人的に, 今後の先の向きが予想できるし, もう悪化具合が見てられなくなったためです. 中途半端なデータでごめんなさい.

それぞれ, バージョンについては以下の通り.

• v0.4.0 .. 早かったけどバグのあるバージョン
• v0.4.1 .. バグ修正のためにパフォーマンスが劣化してしまったバージョン
• current .. 今回の修正

また, 計測は最低 10 回実施しており, 線の色はそれぞれ以下を示しています.

• min .. 最短の結果
• max .. 最長の結果
• mean .. 結果の平均

横軸は $N$, 縦軸は所要時間 (ms) です.
計測に際し, 値数 $N$ の完全ランダムなオブジェクトを作るようなロジックを組みました.
これは単純に 実利用において一番ブレやすい変数が値数であるかなと思ったためです.

改善結果として, min-max の分散が激しかった従来に比べ, 結果は分散が極端に少なくなり, 安定した速度を叩き出せるようになりました. また, $N=5000$ 以下までは改善前と比べて早い結果になりました.

反面, $N=5000$ を超えると勾配が急になっていく様子が見られるため, どこかで累乗の指数が上がった, もしくは軽減できていないことが読み取れると思います.

実際の PR において, 修正後のコードでのパフォーマンスの問題が CodeRabbit によって指摘されました.

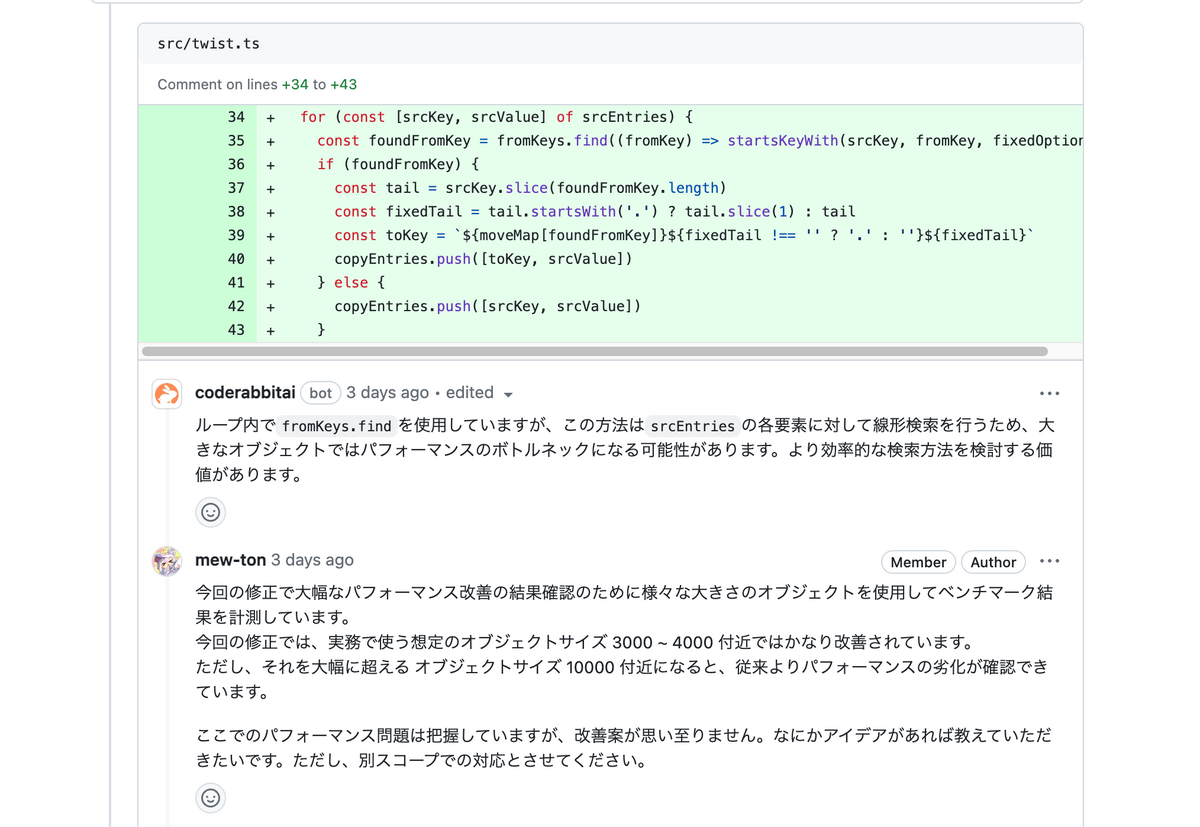
実務での利用は $N=3000 ... 4000$ 付近であるため, 一旦はこれでヨシとし, 別の issue としてこれを対処する方針としました.

CodeRabbit はこういう所を目ざとく見つけてくれるので, 大変助かりますね.

まとめ

今回は, 計算複雑性理論について, 軽くではあるけどしっかり向き合い, パフォーマンス貢献のための緒をみつけるのに役立てました.

計算だけでもだいぶしんどかった. でも, こういう計算を一度はしっかり理解しておくと, 今後パフォーマンスの悪いコードをコーディング・レビュー単位で防げるため, やってよかったと思ってます.

---

株式会社hacomonoでは一緒に働く仲間を募集しています。
採用情報や採用ウィッシュリストもぜひご覧ください！